This week I covered Chapters 13 and 14 of Learning Processing. I did fall a little behind schedule so I am posting this a little late. According to the syllabus, I was also supposed to cover the Chapter on Vectors in “The Nature of Code” but I already covered that two weeks ago.
A lot of what was covered last week in the Introduction to “The Nature of Code” is dealt with in Chapter 13 entitled Mathematics. I did not touch some of the content in more detail so I will do that now.
Last week, we delved a little on randomness and how randomness as modeled using some mathematical algorithms is not entirely random. Over time, if the random() function in Processing is run for a long enough time, a certain pattern would emerge. This means that random() produces a “uniform” distribution of numbers. When it comes to coding a natural-looking simulation, most so than often we will want to create a non-uniform distribution. In other words, we would like to create some numbers that tend to be favored over others. Dr. Shiffman offers two strategies to manipulate our random() into behaving more naturally by making use of probabilities in our code. The first one is to create an array where some numbers are more frequent than others and invoke a conditional that would do a block of code if one of these more frequent numbers is chosen by random(), type casted as integer. The second option is to let random() choose a number between 0 and 1 and create a series of conditionals that test for whether the random number is below or above a certain range, i.e. if n is between 0.00 and 0.60, the outcome under this conditional would have 60% chance of happening.
Another important concept is the alternative use of the noise(), which implements the Perlin noise algorithm, because in contrast to random(), the produced numbers constitute a “smoother” sequence. But noise() operates a little different because its argument is time. Noise() always outputs a number between 0 and 1. And we must scale it, ideally according to the dimensions of our sketch window.
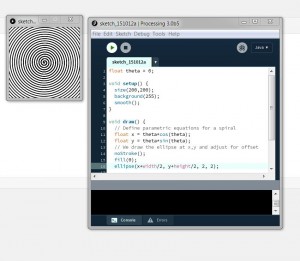
After the discussion on randomness and noise, Chapter 13 reviews a few key ideas on trigonometry and oscillation and how sines and cosines are very well tailored for making elegant animations because they are such well behaved functions. Even though, Processing uses a cartesian coordinate system, we can easily use polar coordinate equations and convert them to cartesian when drawing shapes. Here is my solution to an exercise for creating a spiral in Processing. The idea is to draw a circle following the path traced by the spiral:
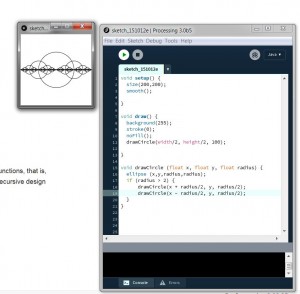
The final topic we covered was Recursion and the coding of recursive functions, that is, functions that call themselves in their definition. Here is a solution to a recursive design problem in the book involving circles:
Chapter 14 mainly talks about the use of transformations to translate, rotate, and scale our sketches as well as the use of transformation matrices in Processing. If you reference my solution to Exercise 13.5, you’ll see that I had to make an offset of width/2 for the x coordinate of the center of each circle and height/2 for the y coordinate since our parametric equation for the spiral produces the spiral around (0,0) and in the Processing coordinate system our (0,0) is at the top left corner. A transformation function like translate() allows us to change the center of our coordinate system and put it whereever we like, offsetting the geometry on the canvas accordingly. Similarly rotate() allows us to rotate our coordinate system and make our composition rotate about an angle. Since functions like translate() and rotate() are additive and affect any shape that is drawn after they are called, Processing provides us with means to separate, save and restore transformation matrices so that we can tailor our transformations selectively as we like. Al
I didn’t have time to incorporate Perlin noise() or beginShape into a particle system like the project for this week calls for. But I wanted to implement the use of pushMatrix and popMatrix into a sketch so I did the following composition
See you next week.